Principal Componential Algorithm (PCA)
今天学习的是无监督学习中的第二类算法:Dimentionality Reduction,即维度降低。我们所研究的数据集合,每个数据通常都有一个特征向量,在真实的问题中,维度往往很高,数量级可以达到上万或者更高。有时候就需要进行降维,好处有这几点:
- Data Compression。数据压缩,大量的数据,每个数据都有很高的特征维度,存储所需要的空间就会很大,对硬件的配置要求也会很高。
- Speed up learning。加速学习、提高训练的速度。
- Visualization。视觉化是处理问题一个很好的手段,形成图形后可以直观地观察、更好地理解我们的问题。当特征向量超过三维后,就无法用图形表示了,所以这类降维往往需要降到三维以下。
数据降维的原理: 特征向量不同分量之间,往往有一定**的相关性。
最简单的例子,我们要表示一根指挥棒,纵坐标为用inch表示其长度,横坐标用cm表示其长度,这样可以形成用二维特征向量表示的特征值。所有的数据都落在一条直线上,事实上也就是一维图形了。
假如相关度不如上个例子那么高,我们还是可以找出一条直线进行拟合,然后将所有数据投射到这条直线上,用这些投射点作为降维之后的数据。同理,对于维度为3的特征向量,可以投射到一个平面(plane)上,降为二维。
PCA: 全称是Principal Componential Algorithm,是目前使用最广泛、最常用的数据降维算法。我们来通过下图说明一下PCA要做什么:
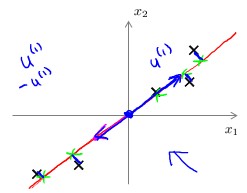
上图中,x1和x2为特征向量的两个分量,坐标系中分布着我们的数据。我们的目的就是寻找这样一条直线(一个一维的向量),使得每个数据点到直线的平均距离最小。同样的,要把n为特征向量降为k维,需要找到k个向量,每个向量用u(i)表示。
###PCA与linear regression(线性回归)的关系
二者都是在坐标系中寻找一个拟合surface,但有以下区别:
- linear regression的坐标系中有y,pca中没有。
- linear regression中的距离,所有x点对应的真实值y=g(x)与估计值f(x)之间的vertical distance距离。
###PCA流程
首先要对数据进行预处理,以使得后面的计算更方便。预处理方法有两个:
- mean normalization。 计算各特征的平均值,记为μj ,(Xj(i)表示第i个样本的第j维特征的value)
μj = Σm Xj(i)/m,然后令Xj(i)= (Xj(i)-μj)。使得各特征的平均值为0. - feature scaling。不同的特征分量,其取值范围不同,比如0-1000、0-1000000,feature scaling的目的就是要使所有特征分量的取值范围相同。方法是:令
Xj(i)= (Xj(i)-μj)/sj。
下面进入PCA核心部分。
计算n*n的协方差矩阵Σ。
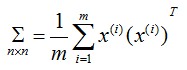
计算Σ的eigenvectors。
[U,S,V]=SVD(Σ)。这是octave中的计算式。SVD为奇异值分解(singular value decomposition),) 。 其中U为n*n的矩阵,取前k列,就得到我们需要的k个向量,这k个向量构成的矩阵我们记为Ureduce。计算每个数据降维后的特征向量表示。
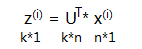
现在讨论几个相关的问题。
###K值大小的确定
首先给出下式:
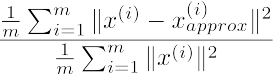
分子叫做:average squared projection error.
分母叫做:total variance.
分式叫做:error ratio. 由于降维后肯定会有信息量的损失,error ratio就是衡量损失的大小。我们需要确定一个threshold,使得当我们使用这k个主成分时,error ratio < threshold,否则信息量损失太大。例如,error ratio<0.01,我们也说,99% of variance is retained。
从上面[U,S,V] = SVD(Σ)返回值中有一个S。S是一个对角阵。可以证明:
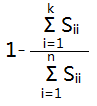
这样,只要返回一个S,我们就可以按照上式进行计算,将k从1逐渐增大,直到符合要求。
###Reconstruction from compressed representation
特征向量从n维降到k维后,我们需要再恢复到n维怎么办?
xapprox = (U')-1×z = (U-1)-1×z = Uz
这里的xapprox是x的近似值。
###PCA的错误使用
既然PCA可以降维,可不可以用来prevent overfitting呢?不能!因为降维时没有考虑到y。应该首选regularization来解决overfitting。
不要盲目用PCA。能用原始数据的尽量用原始数据,当存储量不够、学习缓慢时,可以考虑使用PCA。
###遗留问题
这个课程里并没有详细讲解PCA算法细节,只是给了octave中用到的公式。算法细节需要另外找资料学习。