大规模机器学习

机器学习在这几年得到快速发展，一个很重要的原因是 Large Dataset（大规模数据），这节课就来介绍用机器学习算法处理大规模数据的问题。

关于数据的重要性，有一句话是这么说的：

It’s not who has the best algorithm that wins.
It’s who has the most data.

然而，当数据量过大时，计算的复杂度会增加，计算成本也会提高。假如数据量是一百万，使用梯度下降算法来训练参数，每走一步，需要对百万数据进行求和计算，这样的计算量是极大的。但现实问题总是有大量数据，比如全国的车辆、网民等等。那么，我们就有必要研究一下如何更好地处理大规模数据。

###方案一：Stochastic Gradient Descent

以 linear regression 为例，先开看看我们原来的梯度下降算法：

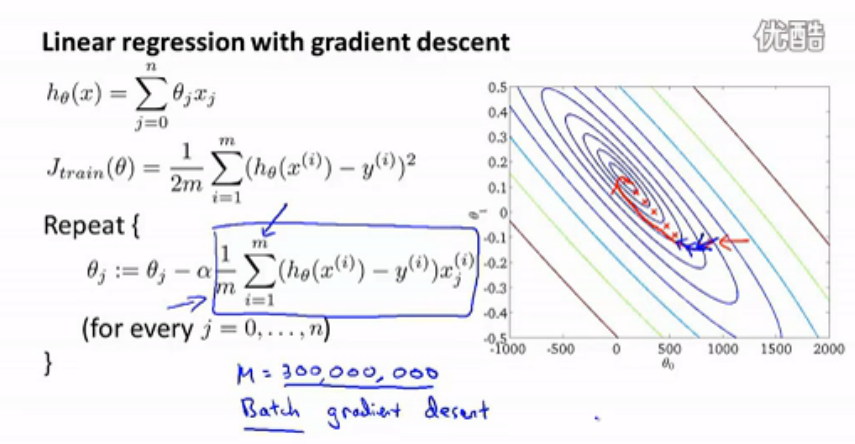
图中给出了要求的model h(x)、目标函数J、以及梯度下降算法（循环部分）。迭代的过程：每一步使用所有数据计算θ，并重新赋值，然后下一步再使用所有数据和上一步求得的θ更新θ。图中右侧，中心点是最优点，θ从起始点，每迭代一步就像中心点移动一步，最终走到中心点求出θ最优值。这里的问题是，每迭代一步，就需要计算所有数据（如百万数据）。

上述梯度下降算法也叫 batch gradient descent 。下面我们做些改进，以适应大数据的情况。

上图右侧，我们改变了迭代形式。对于训练集中每个数据，fit θ，使得模型符合这个数据，然后用第二个数据走同样步骤，以此类推。也就是说，每个数据都能获得目前为止最优的θ。这样的迭代，我们称为 stochastic gradient descent 。

需要注意：迭代之前，需要 randomly shuffle training example. 因为数据的不同使用次序，得到的结果不尽相同。

下面给出该算法的步骤和演示图：

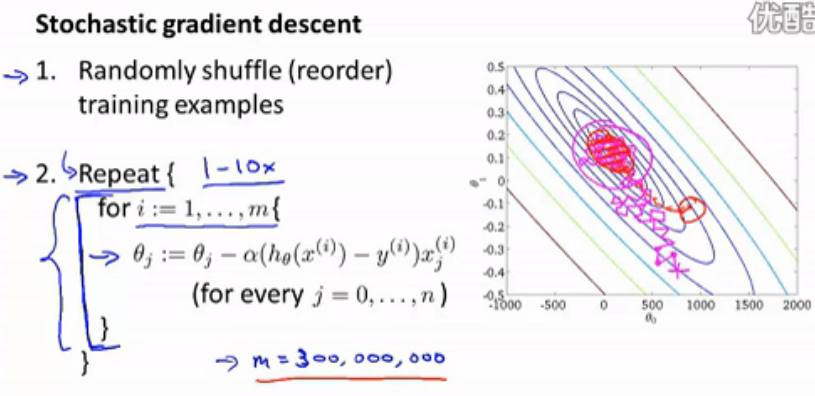
从演示图可以看出，θ最后可能围绕最优点左右摇摆而达不到最优点。θ甚至可能不会converge。那么，怎么检查θ能否converge呢？

每迭代n个数据（eg.1000），使用目前得到的θ，计算这n个数据的cost，并绘制在横坐标为迭代次数、纵坐标为cost的坐标系中。随着迭代次数增加，坐标系中的曲线越来越长。观察曲线形状，如果一直呈下降趋势，那么说明可以converge，如果一直上下摇摆或者上升趋势，就说明无法converge。对于后者，可以随着迭代次数的增加逐渐减小α（学习速度），就可以保证θ可以converge。

一个应用：Online learning

Online learning 是根据不断涌入的新数据更新θ从而改进我们的model。例如一个货运订单系统，用户输入出发地、目的地，网站会给出价格，用户会选择下单或取消。这里的model就是，给出用户特征和出发地、目的地，通过model得出适当价格。这是一个 logistic regress 问题。每当有一个用户进行上述行为，我们的训练集就动态增加了一个数据，这样就可以使用 stochastic gradient descent 动态优化model。

###方案二： Mini-Batch Gradient Descent

在 batch gradient descent 中，我们每次迭代使用全部m个数据。

在 stochastic gradient descent 中，每次迭代使用1个数据。

在 Mini-Batch Gradient Descent 中，每次迭代用b（2-m）个数据，算作一种折中方案。b即为 mini-batch 。

结合上面两个算法，第三个算法很容易理解，如下：

###方案三：Map Reduce and Data Parallelism

当数据量很大，我们又希望使用 batch gradient descent 时，可以将数据分割并分布到不同 的机器上进行局部运算，然后汇总。

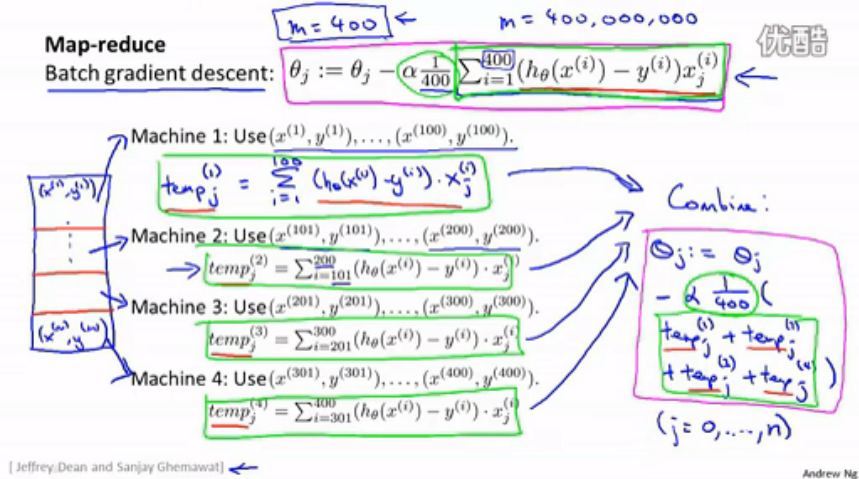
图中，把迭代式加和的部分分割开，400个数据分布到4台机器上，每台机器同步处理100个数据，
最后将四个结果再相加，得到迭代式中加和项的结果。

总的来说，对于大数据，或者分布到不同机器上同步处理，或者使用单数据迭代的算法。