k-means algorithm
最近在学习『机器学习』这门课,使用的斯坦福大学Andrew Ng在Coursera的在线课程。机器学习主要包括有监督学习和无监督学习。我的学习进度到了后者。今天学习的是无监督学习中最常见、最普遍、最基础的一类问题——clustering。
首先说说什么是有监督学习和无监督学习。
给出一个数据集合,如果对于集合中的每个数据,不仅有该数据的特征值向量,而且每个数据都进行了类型标记,我们把这个集合叫做训练集(training set)。然后我们通过一些算法进行学习。学习的目的是,找到一个判别函数,给定一个新的数据,这个判别函数能输出这个数据的所属分类。找到这样的判别函数的过程,就叫做有监督学习。这里的监督,指的是训练集中的每个数据都进行了类别标记。
与此相反,对于无监督学习,每个数据并没有进行类别标记,我们只知道它的特征向量,并不知道所属类别。
所谓clustering(聚类),就是给定一个数据集合,集合大小为m,每个数据都有特征向量x,我们通过某种算法,将这批数据瓜分成k组,每个数据分别属于某一组。
下面直观地说明一下什么是聚类问题,以及聚类的流程。
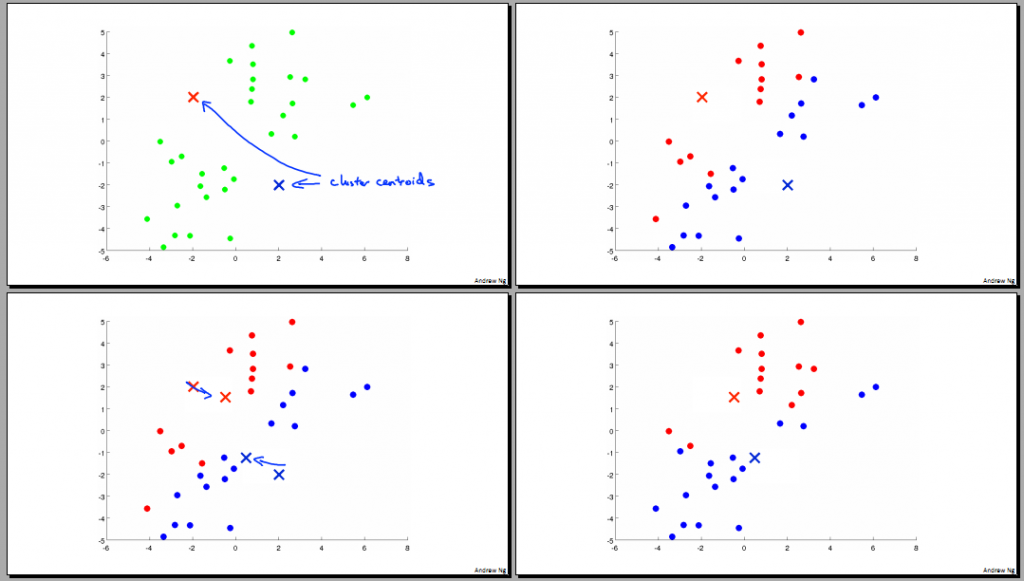
左上角的图中,绿点表示我们的数据集合,横、纵坐标分别是数据的特征值向量分量。例如,数据表示衬衫的尺寸(L/M/S),横、纵坐标分别表示height和weight。我们的目的是将这批数据分为k组(比如3组,L/M/S)。
聚类的过程如下:
- 随机选择两个location,作为class centroid(种子)。如左上图中蓝色和红色x。
- 对于数据集合中的每个数据点,分别计算到两个种子的距离,并互相比较,如果距离蓝色种子近则标记为蓝色,否则标记为红色。如右上图。这个过程叫class assignment。
- 计算每一临时组的中心点(average),并作为这一组新的种子。如左下图,种子移动到了中心点。
- 重复2、3,直到种子不再变动。
在有监督学习中,有个cost function,用J表示。学习的过程,就是不断调整参数,使得J最小。在无监督学习中,也有类似的cost function,在k-means中,我们把它叫做distortion cost function。如图:
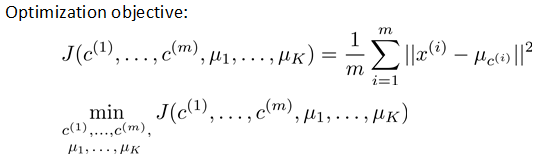
式子右边,表示的是每个点到它所属分组的种子的距离平均值,也就是要最小化这个距离。这里的参数,就是种子的位置和每个数据所属分组。
k-means算法的几个问题
如何选择k的大小?
Andrew Ng说并没有最好的办法。但有以下3个方法可以考虑:
- 观察数据分布大致情况,manually set the number k.
Elbow method。如图:
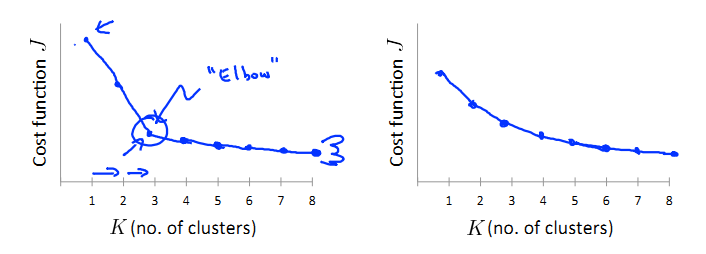
我们对k取不用的值,分别计算相应的J(cost function),绘制图像,转弯最急的那点就是elbow(类似人的胳膊肘)。缺点是,有些根本找不到明确的elbow点,如第二个图。purpose。我们进行聚类,一般都是要服务于某个目的或用途。因此,可以根据具体的用途确定k的大小。比如对于衬衫,是分为3类好还是分为5类好,要看哪一个能更好地服务于我们的应用。
如何确定k个种子的初始位置?
Ng教授给出以下建议:
- K < m,组数要比数据集合的大小小。
- 从数据集合中,随机选取k个。
- 这k个数据就是初始的k个种子。
由于种子的初始位置对于聚类结果影响很大,不同的初试位置聚类的效果好坏也不同。我们可以进行多次聚类,每次选择不同的初始种子,然后选择J最小的那次聚类。
k-means算法的演示地址:K-means - Interactive demo