协方差矩阵的实例与意义
在机器学习中经常需要计算协方差矩阵,本科时没学过这个概念,一直对此非常头疼。现在试图通过实例的计算、图形化的表示来梳理一下什么是协方差矩阵。
###A numerical example
问题:
有一组数据(如下),分别为二维向量,这四个数据对应的协方差矩阵是多少?

解答:
由于数据是二维的,所以协方差矩阵是一个2*2的矩阵,矩阵的每个元素为:
元素(i,j) = (第 i 维所有元素 - 第 i 维的均值) * (第 j 维所有元素 - 第 j 维的均值) 。
其中「*」代表向量内积符号,即两个向量求内积,对应元素相乘之后再累加。
我们首先列出第一维:
D1: (1,3,4,5) 均值:3.25
D2: (2,6,2,2) 均值:3
下面计算协方差矩阵第(1,2)个元素:
元素(1,2)=(1-3.25,3-3.25,4-3.25,5-3.25)*(2-3,6-3,2-3,2-3)=-1
类似的,我们可以把2*2个元素都计算出来:
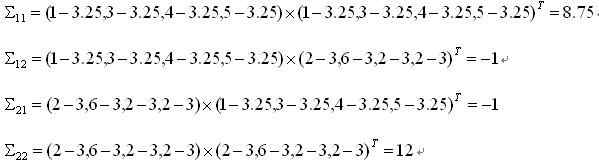
这个题目的最终结果就是:

###An explanation
我们来分析一下上面的例子。首先看一下元素(1,1)的计算过程:
把所有数据的第一个维度拿出来,求出均值,之后的求解过程完全是我们熟悉的「方差」的求法。也就是说,这完完全全就是在求所有数据第一维元素(共4个)的方差(8.75)嘛。类似地,元素(2,2)求的是第二维(共4个)元素的方差(12)。
再来看元素(1,2),这分明就是我们高数里面学的求 x 和 y 的协方差,不再单独计算某一维度的分散程度,而是把两个维度的分散值结合起来,这里才真正体现了「协方差矩阵」中「协方差」的意味。从计算过程和计算结果都能看出,元素(2,1)与元素(1,2)是一样的。也就是说,所有协方差矩阵都是一个对称阵。
总结一下协方差矩阵的特点:
- 对角线元素(i,i)为数据第 i 维的方差。
- 非对角线元素(i,j)为第 i 维和第 j 维的协方差。
- 协方差矩阵是对称阵。
现在只需要了解这些就够了。
###A vivid reprensatation
这里借鉴一下模式识别课件中的五个图来形象地展示一下不同的协方差矩阵代表了什么。这几个都是二维的高斯分布(正态分布),每个例子中有三个分布,分别给出了均值和协方差矩阵。均值代表正态分布的中心点,方差代表其分布的形状(黑色的分割线请 ignore)。请欣赏:





从这五个图可以看出:
- 均值为分布的中心点位置。
- 对角线元素决定了分布图形是圆还是扁。
- 非对角线元素决定了分布图形的轴向(扁的方向)。