LeetCode-Largest Rectangle in Histogram
Largest Rectangle in Histogram
##题目
####Largest Rectangle in Histogram
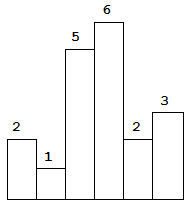
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
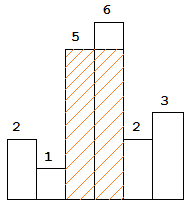
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given height =[2,1,5,6,2,3],
return10.
##解题思路
该题求最大面积的矩形,比较容易理解的思路,就是从每一个bar往两边走,以自己的高度为标准,直到两边低于自己的高度为止,然后用自己的高度乘以两边走的宽度得到矩阵面积。因为我们对于任意一个bar都计算了以自己为目标高度的最大矩阵,所以最好的结果一定会被取到。每次往两边走的复杂度是O(n),总共有n个bar,所以时间复杂度是O(n^2)。
这边在求一个bar左边低于自己高度的最大x位置和右边低于自己高度的最小x位置时,可以采用栈来求解。以求解左边为例:如果栈顶的位置高度比bar的高度高,则不断出栈,如果栈为空,说明bar的左边界能达到最左边位置,则令其left=-1,否则栈顶的位置就是bar的左边界,然后将bar压入栈中,在求解下一个bar的左边界,这样遍历一遍就知道每个bar的左边界位置。
同理可以求解每个bar的右边界位置。这样每个bar能形成的最大矩形面积为height(bar)*(right-left-1),整个时间为O(n)+O(n)+O(n),分别为求左边界,求右边界,求最大面积,这样总的时间复杂度为O(n).
下一题Maximal Rectangle是该题的扩展,该题是其子程序。
##算法代码
代码采用JAVA实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60public class Solution {
public int largestRectangleArea(int[] height) {
if(height==null || height.length==0)
return 0;
if(height.length==1)
return height[0];
//使用栈来求解每个bar左边高度小于H(bar)的最大的x坐标,记为left
int[] left=new int[height.length];
LinkedList<Integer> stack=new LinkedList<Integer>();
stack.push(0);
for(int i=0;i<height.length;i++)
{
while(stack.size()!=0 &&(height[stack.peek()]>=height[i]))
{
stack.pop();
}
if(stack.size()==0)
{
left[i]=-1;
stack.push(i);
}
else
{
left[i]=stack.peek();
stack.push(i);
}
}
//同理使用栈来求解每个bar右边高度小于H(bar)的最小的x坐标,记为right
int[] right=new int[height.length];
LinkedList<Integer> stack2=new LinkedList<Integer>();
stack2.push(height.length-1);
for(int i=height.length-1;i>=0;i--)
{
while(stack2.size()!=0 &&(height[stack2.peek()]>=height[i]))
{
stack2.pop();
}
if(stack2.size()==0)
{
right[i]=height.length;
stack2.push(i);
}
else
{
right[i]=stack2.peek();
stack2.push(i);
}
}
//计算每个bar能形成的矩形的面积,并求得一个最大面积
int maxRec=0;
for(int i=0;i<height.length;i++)
{
int rec=(right[i]-left[i]-1)*height[i];
maxRec=Math.max(maxRec,rec);
}
return maxRec;
}
}